支援向量機(Support Vector Machine)

監督式學習的演算法，排序學習中之逐點式學習(pointwise)可運用支援向量機進行訓練。

支援向量機是一種最大邊界(Large-Margin)的分類器，由Vapnik及其在AT&T Bell實驗室之團隊所共同發展之技術[Boser et al. 1992; Cortes & Vapnik 1995]。

決定函數為一個超平面(Hyper-plane)，決定函數切割n維空間，使所有的資料點由決定函數區分為不同類別。

以兩個類別來說，分別在兩類別中，所有距離最接近決定函數所形成超平面之數個資料點，稱之為支援向量(Support Vectors)。

此超平面至分屬不同類別之支援向量的距離和，則稱之為邊界，好的分類邊界要距離最近的訓練資料點越遠越好，可以減低判斷錯誤的機率。

實線為我們找出的 Hyper-plan，而我們將 H1 與 H2 稱之為 Support Hyper-plans，而我們希望能夠找出最佳的 Classification Hyper-plan 使兩 Support Hyper-plans 之間有最大的邊距。

H1 到原點的距離為： |1− b| / ||w|| ；H2 到原點的距離為： |−1−b| / ||w|| ，因此 H1 與 H2 之間的距離為 。邊距的大小會是，因此極大化邊距就是極小化，由於||w||是一個單調函數，我們可以對其加入平方，和前面的係数，這個式子是為了方便求導。

在附加限制條件下最小化函数：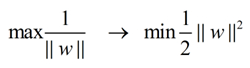

即：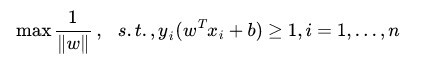

这是一個拉格朗日優化问题，可以通過拉格朗日乘數法得到最優超平面的權重向量W和偏置b。